Abstract
This project aims to link two of the things i'm very interested in : artificial intelligence and robotics. In this paper I will use the openAI Gym python library and one of it's environment : Bipedal Walker (Box2D environments).
The final goal is to have a pseudo-robotic agent that can walk from point A to point B. The agent will “learn” how to walk using the process of reinforcement learning (Deep Q-learning in our case and not only Q-learning). The agent is defined as pseudo-robotic because accroding to the definition : “ A robot is a machine that resembles a living creature in being capable of moving independently (as by walking or rolling on wheels) and performing complex actions (such as grasping and moving objects) “ - Merriam-Webster (https://www.merriam-webster.com/dictionary/robot). So pseudo-robotic because it’s a simulation of this machine.
In this post I will go though multiple topics :
- Short definition of reinforcement learning
- Description of the environment and the agent
- Explaining DDPG algorithm
- Implementation of the environment and simulation
You are welcome to go and see the OpenAI Gym documentation here : https://www.gymlibrary.ml/environments/
Reinforcement Learning - what you need to know
The history of reinforcement learning (RL) has two main threads, both long and rich, that were pursued independently before intertwining in modern reinforcement learning. One thread concerns learning by trial and error and started in the psychology of animal learning. This thread runs through some of the earliest work in artificial intelligence and led to the revival of reinforcement learning in the early 1980s. The other thread concerns the problem of optimal control and its solution using value functions and dynamic programming. For the most part, this thread did not involve learning. Although the two threads have been largely independent, the exceptions revolve around a third, less distinct thread concerning temporal-difference methods such as used in the tic-tac-toe example. All of the threads came together in the late 1980’s to produce the modern field of reinforcement learning as we know it.
Today, reinforcement learning is the training of machine learning models to make a sequence of decisions. The agent learns to achieve a goal in an uncertain, potentially complex environment.
The underlying maths in RL is based on Markovian Decision Processes (MDP) :
- a set of environments and agent state S;
- a set of actions A on the agent;
- the probability of transition from a state s to a state s’
- the immediate reward after transition from s to s’ with action a.
The purpose of reinforcement learning is for the agent to learn an optimal, or nearly-optimal, policy that maximizes the “reward function” or other user-provided reinforcement signal that accumulates from the immediate rewards.
This concludes our short recap of what you need to know in RL.
Description of the Environment and the agent
This is a simple 4-joint walker robot environment. There are two versions :
- Normal, with slightly uneven terrain
- Hardcore, with ladder, stumps, pitfalls
To solve the normal version, you need to get 300 points in 1600 time steps. To solve the hardcore version, you need 300 points in 2000 time steps.
Action Space
Actions are motor speed valued in the [-1, 1] range for each of the 4 joints at both hips and knees
Observation Space
State consists of hull angle speed, angular velocity, horizontal speed, vertical speed, position of joints and joints angular speed, legs contact with ground, and 10 lidar rangefinder measurements. There are no coordinates in the state vector.
Reward
Reward is given for moving forward, totaling 300+ points up to the far end. If the robot falls, it gets -100. Applying motor torque costs a small amount of points. A more optimal agent will get a better score.
Starting State
The walker starts standing at the left end of the terrain with the hull horizontal, and both legs in the same position with a slight knee angle.
Episode Termination
The episode will terminate if the hull gets in contact with the ground or if the walker exceeds the right end of the terrain length.
Explaining the DDPG algorithm
Deep Deterministic Policy Gradient (DDPG) is an algorithm which concurrently learns a Q-function and a policy. It uses off-policy data and the Bellman equation to learn the Q-function, and uses the Q-function to learn the policy.
This approach is closely connected to Q-learning, and is motivated the same way: if you know the optimal action-value function then in any given state, the optimal action can be found by solving :
a(s) = argmax_a Q(s,a).
DDPG interleaves learning an approximator to Q(s,a) with learning an approximator to a(s), and it does so in a way which is specifically adapted for environments with continuous action spaces. But what does it mean that DDPG is adapted specifically for environments with continuous action spaces? It relates to how we compute the max over actions in max_a Q*(s,a).
The Q-learning side of DDPG
Trick One : Replay Buffers. All standard algorithms for training a deep neural network to approximate Q*(s,a) make use of an experience replay buffer. This is the set D of previous experiences. In order for the algorithm to have stable behavior, the replay buffer should be large enough to contain a wide range of experiences, but it may not always be good to keep everything.
If you only use the very-most recent data, you will overfit to that and things will break; if you use too much experience, you may slow down your learning. This may take some tuning to get right.
Trick Two : Target Networks. Q-learning algorithms make use of target networks. The term
r + gamma (1 - d) max_a’ Q_phi(s’,a’)
is called the target, because when we minimize the MSBE (Mean squared Bellman error) loss, we are trying to make the Q-function be more like this target.
Problematically, the target depends on the same parameters we are trying to train: phi. This makes MSBE minimization unstable. The solution is to use a set of parameters which comes close to phi, but with a time delay—that is to say, a second network, called the target network, which lags the first.
Policy Learning of DDPG
Policy learning in DDPG is fairly simple. We want to learn a deterministic policy mu_theta(s) which gives the action that maximizes Q_phi(s,a). Because the action space is continuous, and we assume the Q-function is differentiable with respect to action, we can just perform gradient ascent (with respect to policy parameters only) to solve the maximization problem.
Implementation of the Environment and simulation
Problem Statement
Teach the bipedal robot to walk from a starting point to end without falling, and maximize the reward. Reward if given form oving forward (total +300 pts). If the robot falls, the sum of the rewards will decrease from 100 pts. Applying motor torque costs a small amount of points.
Common Algorithms
Deterministic policy maps state to action without uncertainty. It happens when you have a deterministic environment like a chess table. Stochastic policy outputs a probability distribution over actions in a given state.
A model of the environment means a function which predicts state transitions and rewards. Model-free RL algorithms are those that make no effort to learn the underlying dynamics that govern how an agent interacts with the environment.
Policy gradient algorithms utilize a form of policy iteration: they evaluate the policy, and then follow the policy gradient to maximize performance.
In Q learning, We constantly update a Q-Table, which is a lookup table where we calculate the maximum expected future rewards for action at each state. Basically, this table will guide us to the best action at each state.
Off-policy algorithms generally employ a separate behavior policy that is independent of the policy being improved upon; the behavior policy is used to simulate trajectories. A key benefit of this separation is that the behavior policy can operate by sampling all actions, whereas the estimation policy can be deterministic
The TD error signal is excellent at compounding the variance introduced by your bad predictions over time. It is highly suggested to use a replay buffer to store the experiences of the agent during training, and then randomly sample experiences to use for learning in order to break up the temporal correlations within different training episodes. This technique is known as experience replay.
Actor-critic combines the benefits of both approaches from policy-iteration method as PG and value-iteration method as Q-learning. The network will estimate both a value function V(s) (how good a certain state is to be in) and a policy π(s).
The critic’s output is simply the estimated Q-value of the current state and of the action given by the actor. The deterministic policy gradient theorem provides the update rule for the weights of the actor network. The critic network is updated from the gradients obtained from the TD error signal.
DDPG algorithm is an actor-critic algorithm; it primarily uses two neural networks, one for the actor and one for the critic. These networks compute action predictions for the current state and generate a temporal-difference (TD) error signal each time step. The input of the actor network is the current state, and the output is a single real value representing an action chosen from a continuous action space. :::
Implementing the Model
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
# CREDITS GO TO THIS PERSON -> https://github.com/shivaverma/OpenAIGym/tree/master/bipedal-walker
# I used and personallized the code but the idea comes from the github and the references at the end.
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
class Actor(nn.Module):
def __init__(self, state_size, action_size, seed, fc_units=600, fc1_units=300):
super(Actor, self).__init__()
self.seed = torch.manual_seed(seed)
self.fc1 = nn.Linear(state_size, fc_units)
self.fc2 = nn.Linear(fc_units, fc1_units)
self.fc3 = nn.Linear(fc1_units, action_size)
self.bn1 = nn.BatchNorm1d(fc_units)
self.bn2 = nn.BatchNorm1d(fc1_units)
self.reset_parameters()
def forward(self, state):
"""Build an actor (policy) network that maps states -> actions."""
x = F.relu((self.bn1(self.fc1(state))))
x = F.relu((self.bn2(self.fc2(x))))
return F.torch.tanh(self.fc3(x))
class Critic(nn.Module):
def __init__(self, state_size, action_size, seed, fcs1_units=600, fcs2_units=300, fca1_units=300):
super(Critic, self).__init__()
self.seed = torch.manual_seed(seed)
self.fcs1 = nn.Linear(state_size, fcs1_units)
self.fcs2 = nn.Linear(fcs1_units, fcs2_units)
self.fca1 = nn.Linear(action_size, fca1_units)
self.fc1 = nn.Linear(fcs2_units, 1)
self.bn1 = nn.BatchNorm1d(fcs1_units)
self.reset_parameters()
def forward(self, state, action):
"""Build a critic (value) network that maps (state, action) pairs -> Q-values."""
xs = F.relu((self.bn1(self.fcs1(state))))
xs = self.fcs2(xs)
xa = self.fca1(action)
x = F.relu(torch.add(xs, xa))
return self.fc1(x)
Implementing the DDPG Agent
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
import numpy as np
import copy
import random
from collections import namedtuple, deque
import torch
import torch.nn.functional as F
import torch.optim as optim
BUFFER_SIZE = 1000000 # replay buffer size
BATCH_SIZE = 100 # minibatch size
GAMMA = 0.99 # discount factor
TAU = 0.001 # for soft update of target parameters
LR_ACTOR = 0.0001 # learning rate of the actor
LR_CRITIC = 0.001 # learning rate of the critic
WEIGHT_DECAY = 0.001 # L2 weight decay
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
## The Agent
class Agent():
# Interacts with and learns from the observation space.
def __init__(self, state_size, action_size, random_seed):
self.state_size = state_size
self.action_size = action_size
self.seed = random.seed(random_seed)
# Actor Network (w/ Target Network)
self.actor_local = Actor(state_size, action_size, random_seed).to(device)
self.actor_target = Actor(state_size, action_size, random_seed).to(device)
self.actor_optimizer = optim.Adam(self.actor_local.parameters(), lr=LR_ACTOR)
# Critic Network (w/ Target Network)
self.critic_local = Critic(state_size, action_size, random_seed).to(device)
self.critic_target = Critic(state_size, action_size, random_seed).to(device)
self.critic_optimizer = optim.Adam(self.critic_local.parameters(), lr=LR_CRITIC, weight_decay=WEIGHT_DECAY)
# Noise process
self.noise = OUNoise(action_size, random_seed)
# Replay memory
self.memory = ReplayBuffer(action_size, BUFFER_SIZE, BATCH_SIZE, random_seed)
def step(self, state, action, reward, next_state, done):
"""Save experience in replay memory, and use random sample from buffer to learn."""
# Save experience / reward
self.memory.add(state, action, reward, next_state, done)
# Learn, if enough samples are available in memory
if len(self.memory) > BATCH_SIZE:
experiences = self.memory.sample()
self.learn(experiences, GAMMA)
def act(self, state, add_noise=True):
"""Returns actions for given state as per current policy."""
state = torch.from_numpy(state).float().unsqueeze(0).to(device)
self.actor_local.eval()
with torch.no_grad():
action = self.actor_local(state).cpu().data.numpy()
self.actor_local.train()
if add_noise:
action += self.noise.sample()
return action
def reset(self):
self.noise.reset()
def learn(self, experiences, gamma):
"""Update policy and value parameters using given batch of experience tuples.
Q_targets = r + γ * critic_target(next_state, actor_target(next_state))
where:
actor_target(state) -> action
critic_target(state, action) -> Q-value
Params
======
experiences (Tuple[torch.Tensor]): tuple of (s, a, r, s', done) tuples
gamma (float): discount factor
"""
states, actions, rewards, next_states, dones = experiences
# ---------------------------- update critic ---------------------------- #
# Get predicted next-state actions and Q values from target models
actions_next = self.actor_target(next_states)
Q_targets_next = self.critic_target(next_states, actions_next)
# Compute Q targets for current states (y_i)
Q_targets = rewards + (gamma * Q_targets_next * (1 - dones))
# Compute critic loss
Q_expected = self.critic_local(states, actions)
critic_loss = F.mse_loss(Q_expected, Q_targets)
# Minimize the loss
self.critic_optimizer.zero_grad()
critic_loss.backward()
self.critic_optimizer.step()
# ---------------------------- update actor ---------------------------- #
# Compute actor loss
actions_pred = self.actor_local(states)
actor_loss = -self.critic_local(states, actions_pred).mean()
# Minimize the loss
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()
# ----------------------- update target networks ----------------------- #
self.soft_update(self.critic_local, self.critic_target, TAU)
self.soft_update(self.actor_local, self.actor_target, TAU)
Training our agent
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
import gym
import torch
import numpy as np
import matplotlib.pyplot as plt
env = gym.make('BipedalWalker-v3')
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
agent = Agent(state_size=state_dim, action_size=action_dim, random_seed=0)
def ddpg(episodes, step, pretrained, noise):
if pretrained:
agent.actor_local.load_state_dict(torch.load('./weights-simple/1checkpoint_actor.pth', map_location="cpu"))
agent.critic_local.load_state_dict(torch.load('./weights-simple/1checkpoint_critic.pth', map_location="cpu"))
agent.actor_target.load_state_dict(torch.load('./weights-simple/1checkpoint_actor_t.pth', map_location="cpu"))
agent.critic_target.load_state_dict(torch.load('./weights-simple/1checkpoint_critic_t.pth', map_location="cpu"))
reward_list = []
for i in range(episodes):
state = env.reset()
score = 0
for t in range(step):
if i%100 == 0:
env.render()
action = agent.act(state, noise)
next_state, reward, done, info = env.step(action[0])
# agent.step(state, action, reward, next_state, done)
state = next_state.squeeze()
score += reward
if done:
if i%10 == 0:
print('Reward: {} | Episode: {}/{}'.format(score, i, episodes))
break
reward_list.append(score)
if score >= 270:
print('Task Solved')
torch.save(agent.actor_local.state_dict(), 'checkpoint_actor.pth')
torch.save(agent.critic_local.state_dict(), 'checkpoint_critic.pth')
torch.save(agent.actor_target.state_dict(), 'checkpoint_actor_t.pth')
torch.save(agent.critic_target.state_dict(), 'checkpoint_critic_t.pth')
break
torch.save(agent.actor_local.state_dict(), 'checkpoint_actor.pth')
torch.save(agent.critic_local.state_dict(), 'checkpoint_critic.pth')
torch.save(agent.actor_target.state_dict(), 'checkpoint_actor_t.pth')
torch.save(agent.critic_target.state_dict(), 'checkpoint_critic_t.pth')
print('Training saved')
return reward_list
scores = ddpg(episodes=100, step=2000, pretrained=1, noise=0)
fig = plt.figure()
plt.plot(np.arange(1, len(scores) + 1), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
Sortie
1
2
3
4
5
6
7
8
9
10
11
Reward: 73.6079639945533 | Episode: 0/100
Reward: 235.62352205739126 | Episode: 10/100
Reward: -78.38845131642697 | Episode: 20/100
Reward: 242.92582461689423 | Episode: 30/100
Reward: 242.2452225192549 | Episode: 40/100
Reward: 239.84728259279626 | Episode: 50/100
Reward: 240.02700733104282 | Episode: 60/100
Reward: 12.12186484878464 | Episode: 70/100
Reward: 235.61126771194634 | Episode: 80/100
Reward: 242.58905712861878 | Episode: 90/100
Training saved
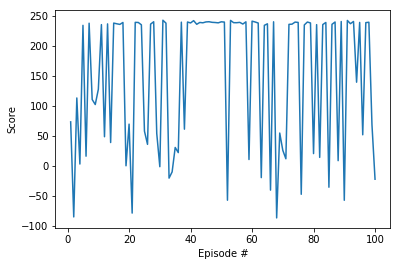
Conclusion
Using DDPG algorithm, it is possible to train a bipedal robot to walk. With just 2000 episodes of training our agent learned to walk considerably well. We’ve seen some ups and down so there’s a ot to do on tweaking the hyperparameters to have a constant improvement in terms of rewards. This Actor-Critic interaction is similar to how GAN’s work (Generative Adversarial Networks). A post will soon be posted on this subject.
Next steps
- Apply the model to the hardcore environment
- Apply the model to a real robot
References
Brockman, G., Cheung, V., Pettersson, L., Schneider, J., Schulman, J., Tang, J., and Zaremba, W. (2016). Openai gym. arXiv preprint arXiv:1606.01540.
Catto, E. (2011). Box2d: A 2d physics engine for games.
Emami, P. (2019 (accessed November 17, 2019)). Deep Deterministic Policy Gradients in TensorFlow. https://pemami4911.github.io/blog/2016/08/21/ddpg-rl.html.
open AI (2019 (accessed November 17, 2019)). bipedal walker source. https://github.com/openai/gym/blob/master/gym/envs/box2d/bipedal_walker.py.
openAI (2019 (accessed November 17, 2019)). rl intro2. https://spinningup.openai.com/en/latest/spinningup/rl_intro2.html#citations-below.
Song, D. R., Yang, C., McGreavy, C., and Li, Z. (2017). Recurrent network-based deterministic policy gradient for solving bipedal walking challenge on rugged terrains. arXiv preprint arXiv:1710.02896.
Verma, S. (2019 (accessed November 17, 2019)). teach-your-ai-how-to-walk. https://towardsdatascience.com/teach-your-ai-how-to-walk-5ad55fce8bca.
Mikhail Scherbina (Aug 21, 2019). Introduction to RL (DDPG and TD3) for New Recommendation https://towardsdatascience.com/reinforcement-learning-ddpg-and-td3-for-news-recommendation-d3cddec26011
