Bank loan payment default prediction - EOT Assignement
Predicting bank loan payment default in R, from exploratory analysis through to model comparison.
Context
This project is the end of term assignment in the Discriminant Analysis course led by Prof. Salim Lardjane, UBS.
Goals
The project has 2 main goals:
- be familiar with standard machine learning models
- implement from scratch those algorithms to understand the underlying statistics
Loading in the libraries
We’ll be reading a file containing information regarding the financial situation of a person to know weather this person is fit to pay the default or not.
library(foreign)
library(MASS)
library(ROCR)
library(mlogit)
library(caTools)
library(e1071)
library(ggplot2)
library(ROCit)
library("tidyverse")
data <- read.spss("./bankloan.sav",to.data.frame=TRUE)
Descriptive analysis
summary(data)
## age ed employ
## Min. :20.00 Did not complete high school:460 Min. : 0.000
## 1st Qu.:29.00 High school degree :235 1st Qu.: 3.000
## Median :34.00 Some college :101 Median : 7.000
## Mean :35.03 College degree : 49 Mean : 8.566
## 3rd Qu.:41.00 Post-undergraduate degree : 5 3rd Qu.:13.000
## Max. :56.00 Max. :33.000
## address income debtinc creddebt
## Min. : 0.000 Min. : 13.00 Min. : 0.10 Min. : 0.0117
## 1st Qu.: 3.000 1st Qu.: 24.00 1st Qu.: 5.10 1st Qu.: 0.3822
## Median : 7.000 Median : 35.00 Median : 8.70 Median : 0.8851
## Mean : 8.372 Mean : 46.68 Mean :10.17 Mean : 1.5768
## 3rd Qu.:12.000 3rd Qu.: 55.75 3rd Qu.:13.80 3rd Qu.: 1.8984
## Max. :34.000 Max. :446.00 Max. :41.30 Max. :20.5613
## othdebt default preddef1 preddef2
## Min. : 0.04558 No :517 Min. :0.0001166 Min. :0.0000387
## 1st Qu.: 1.04594 Yes :183 1st Qu.:0.0456301 1st Qu.:0.0351757
## Median : 2.00324 NA's:150 Median :0.1715129 Median :0.1590730
## Mean : 3.07879 Mean :0.2585762 Mean :0.2578660
## 3rd Qu.: 3.90300 3rd Qu.:0.4073259 3rd Qu.:0.4332770
## Max. :35.19750 Max. :0.9993967 Max. :0.9994570
## preddef3
## Min. :0.07464
## 1st Qu.:0.13476
## Median :0.20010
## Mean :0.25858
## 3rd Qu.:0.32863
## Max. :0.94810
Discriminant Analysis without cross-validation
Separating the data (train/test)
library(MASS)
library(e1071)
na <- c(701:850)
apred <- data[na,] # the data that we're going to predict later on, once our models are trained
data2 <- subset(data, data$default != "NA'S") # the data we'll use for the train/test datasets
data2<-data2[1:9]
data2<-data2[-2]
data2[,8]<-as.numeric(data2$default)-1
n = dim(data2)[1]
id = sample(1:n,floor(0.75*n),replace=F)
train <- data2[id,]
test <- data2[-id,]
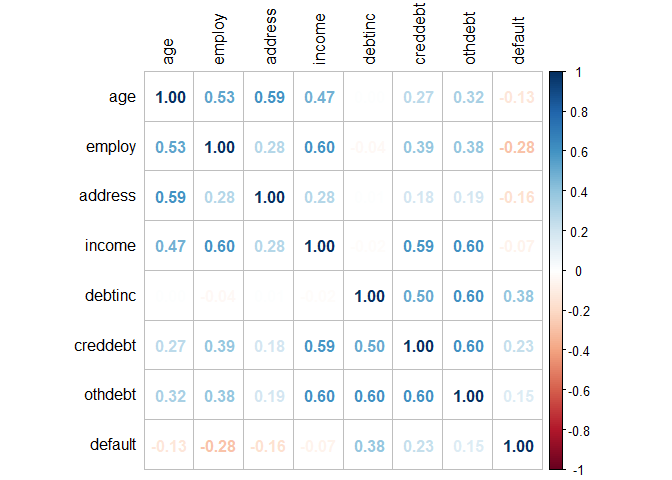
Correlation coefficient visualization
library(corrplot)
corrplot(cor(train), # Correlation matrix
method = "number", # Correlation plot method
type = "full", # Correlation plot style (also "upper" and "lower")
diag = TRUE, # If TRUE (default), adds the diagonal
tl.col = "black", # Labels color
bg = "white", # Background color
title = "", # Main title
col = NULL) # Color palette
Graphs
In order to find the best way to represent our data, we’ll sort the variables in 3 classes : stability, demographic and financial data.
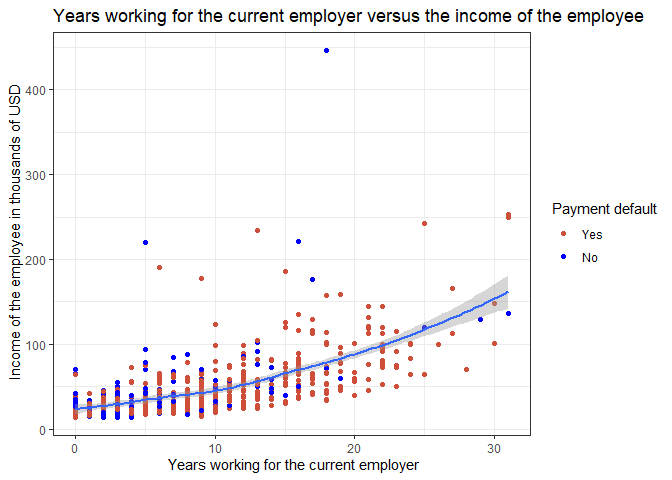
# stability variables : employ address
# demographic variables : age
# financial variables : income debtinc creddebt othdebt
# employ income
data2 %>% mutate(default = factor(default)) %>%
ggplot(aes(x = employ, y = income)) +
geom_point(mapping = aes(color = default)) +
labs(x=" Years working for the current employer",
y=" Income of the employee in thousands of USD",
color = "Payment default") +
geom_smooth() +
scale_color_manual(values = c("0" = "tomato3",
"1" = "blue"),
labels = c("Yes",
"No")) +
theme_bw()+
ggtitle("Years working for the current employer versus the income of the employee")
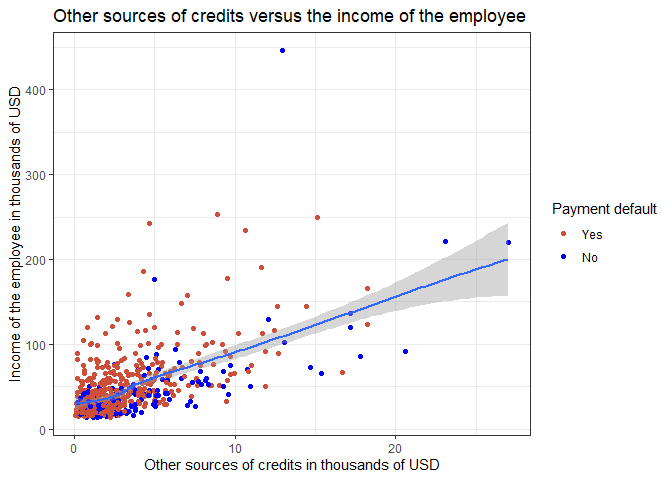
# othdebt income
data2 %>% mutate(default = factor(default)) %>%
ggplot(aes(x = othdebt, y = income)) +
geom_point(mapping = aes(color = default)) +
labs(y="Income of the employee in thousands of USD",
x="Other sources of credits in thousands of USD",
color = "Payment default") +
geom_smooth() +
scale_color_manual(values = c("0" = "tomato3",
"1" = "blue"),
labels = c("Yes",
"No")) +
theme_bw()+
ggtitle("Other sources of credits versus the income of the employee")
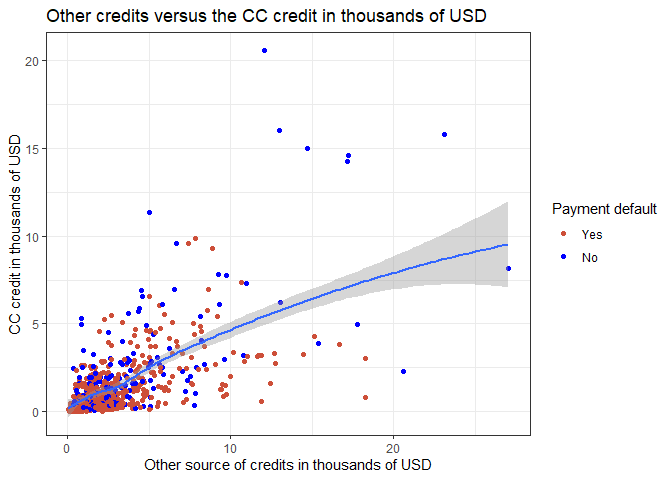
# othdebt creddebt
data2 %>% mutate(default = factor(default)) %>%
ggplot(aes(x = othdebt, y = creddebt)) +
geom_point(mapping = aes(color = default)) +
labs(y="CC credit in thousands of USD",
x="Other source of credits in thousands of USD",
color = "Payment default") +
geom_smooth() +
scale_color_manual(values = c("0" = "tomato3",
"1" = "blue"),
labels = c("Yes",
"No")) +
theme_bw()+
ggtitle("Other credits versus the CC credit in thousands of USD")
Defining the ROC function
This function will allow us to trace a ROC curve for each model that returns posterior probabilities
roc <- function(post1, col){
trapeze <- function(ao,bo) {
k <- length(ao)
iz <- 0
for (i in 1:(k-1)) {
iz <- iz+(ao[i+1]-ao[i])*(bo[i]+bo[i+1])/2
}
return(iz)
}
delta=0.001
valeurs <- seq(0,1,delta)
N <- length(valeurs)
sensibilite <- rep(NA,N)
antispec <- rep(NA,N)
i <- 0
for (u in valeurs) {
i <- i+1
pr2predict <- (post1>u)+0
TN1 <- sum((pr2predict==0)*(test$default==0))
FP1 <- sum((pr2predict==1)*(test$default==0))
FN1 <- sum((pr2predict==0)*(test$default==1))
TP1 <- sum((pr2predict==1)*(test$default==1))
Rap1 <- TP1/(TP1+FN1)
Pre1 <- TP1/(TP1+FP1)
F_sco1 <- (2*TP1)/(2*TP1+FP1+FN1)
Spe1 <- TN1/(FP1+TN1)
Err1 <- ((FP1+FN1)/(TN1+FP1+TP1+FN1)*100)
sensibilite[i] <- Rap1
antispec[i] <- 1-Spe1
}
antispec<- c(0,rev(antispec),1)
sensibilite <- c(0,rev(sensibilite),1)
plot(antispec,sensibilite,type="s",col=col,lwd=1)
return(trapeze(antispec, sensibilite))
}
Defining the models
For each model we’ll compute recall, f-score, acc, specificity and add the values to a dataframe that we’ll comment at the end.
Closest Mean method
no.age <- mean(train[train$default==0,]$age)
yes.age <- mean(train[train$default==1,]$age)
no.employ <- mean(train[train$default==0,]$employ)
yes.employ <- mean(train[train$default==1,]$employ)
no.address <- mean(train[train$default==0,]$address)
yes.address <- mean(train[train$default==1,]$address)
no.income <- mean(train[train$default==0,]$income)
yes.income <- mean(train[train$default==1,]$income)
no.debtinc <- mean(train[train$default==0,]$debtinc)
yes.debtinc <- mean(train[train$default==1,]$debtinc)
no.creddebt <- mean(train[train$default==0,]$creddebt)
yes.creddebt <- mean(train[train$default==1,]$creddebt)
no.othdebt <- mean(train[train$default==0,]$othdebt)
yes.othdebt <- mean(train[train$default==1,]$othdebt)
prediction <- function(x,y,z,a,b,c,d) {
if ((x-yes.age)^2+(y-yes.employ)^2+(z-yes.address)^2+(a-yes.income)^2+(b-yes.debtinc)^2+(c-yes.creddebt)^2+(d-yes.othdebt)^2 >(x-no.age)^2+(y-no.employ)^2+(z-no.address)^2+(a-no.income)^2+(b-no.debtinc)^2+(c-no.creddebt)^2+(d-no.othdebt)^2)
{
return(1)
} else {return(0)}
}
pred <- rep(NA,length(test$default))
for (i in 1:length(test$default)) {
pred[i] <- prediction(test$age[i],test$employ[i],test$address[i], test$income[i], test$debtinc[i], test$creddebt[i], test$othdebt[i])
}
MCPPM = table(pred,test$default)
MCPPMerr = (MCPPM[2,1]+MCPPM[1,2])/sum(MCPPM)
MCPPMrappel = MCPPM[2,2]/(MCPPM[2,2]+MCPPM[1,2])
MCPPMprecision = MCPPM[2,2]/(MCPPM[2,2]+MCPPM[2,1])
MCPPMF = 2*MCPPM[2,2]/(2*MCPPM[2,2]+MCPPM[2,1]+2*MCPPM[1,2])
MCPPMspecificite = MCPPM[2,2]/(MCPPM[2,2]+MCPPM[2,1])
PPM = round(c(MCPPMerr,MCPPMrappel,MCPPMprecision,MCPPMF,MCPPMspecificite),2)
Quadratic Discriminant Analysis method
library(MASS)
model = predict(qda(default~.,train),test)
MCqda = table(test$default,model$class) # correlation matrix
MCqdaerr = (MCqda[2,1]+MCqda[1,2])/sum(MCqda)
MCqdarappel = MCqda[2,2]/(MCqda[2,2]+MCqda[1,2])
MCqdaprecision = MCqda[2,2]/(MCqda[2,2]+MCqda[2,1])
MCqdaF = 2*MCqda[2,2]/(2*MCqda[2,2]+MCqda[2,1]+2*MCqda[1,2])
MCqdaspecificite = MCqda[2,2]/(MCqda[2,2]+MCqda[2,1])
qda = round(c(MCqdaerr,MCqdarappel,MCqdaprecision,MCqdaF,MCqdaspecificite),2)
Linear Discriminant Analysis method
library(MASS)
model = predict(lda(default~.,train),test)
MClda = table(test$default,model$class)
MCldaerr = (MClda[2,1]+MClda[1,2])/sum(MClda)
MCldarappel = MClda[2,2]/(MClda[2,2]+MClda[1,2])
MCldaprecision = MClda[2,2]/(MClda[2,2]+MClda[2,1])
MCldaF = 2*MClda[2,2]/(2*MClda[2,2]+MClda[2,1]+2*MClda[1,2])
MCldaspecificite = MClda[2,2]/(MClda[2,2]+MClda[2,1])
lda = round(c(MCldaerr,MCldarappel,MCldaprecision,MCldaF,MCldaspecificite),2)
Naive Bayes method
library(e1071)
model = predict(naiveBayes(default~.,train),test)
MCbayes = table(test$default,model)
MCbayeserr = (MCbayes[2,1]+MCbayes[1,2])/sum(MCbayes)
MCbayesrappel = MCbayes[2,2]/(MCbayes[2,2]+MCbayes[1,2])
MCbayesprecision = MCbayes[2,2]/(MCbayes[2,2]+MCbayes[2,1])
MCbayesF = 2*MCbayes[2,2]/(2*MCbayes[2,2]+MCbayes[2,1]+2*MCbayes[1,2])
MCbayesspecificite = MCbayes[2,2]/(MCbayes[2,2]+MCbayes[2,1])
bayes = round(c(MCbayeserr,MCbayesrappel,MCbayesprecision,MCbayesF,MCbayesspecificite),2)
K closest neighbours method
library(class)
cl <- as.factor(train$default)
predtest <- knn(train,test,cl, k=1)
MCknn1 = table(test$default,predtest)
MCknn1err = (MCknn1[2,1]+MCknn1[1,2])/sum(MCknn1)
MCknn1rappel = MCknn1[2,2]/(MCknn1[2,2]+MCknn1[1,2])
MCknn1precision = MCknn1[2,2]/(MCknn1[2,2]+MCknn1[2,1])
MCknn1F = 2*MCknn1[2,2]/(2*MCknn1[2,2]+MCknn1[2,1]+2*MCknn1[1,2])
MCknn1specificite = MCknn1[2,2]/(MCknn1[2,2]+MCknn1[2,1])
knn1 = round(c(MCknn1err,MCknn1rappel,MCknn1precision,MCknn1F,MCknn1specificite),2)
predtest <- knn(train,test,cl, k=2)
MCknn2 = table(test$default,predtest)
MCknn2err = (MCknn2[2,1]+MCknn2[1,2])/sum(MCknn2)
MCknn2rappel = MCknn2[2,2]/(MCknn2[2,2]+MCknn2[1,2])
MCknn2precision = MCknn2[2,2]/(MCknn2[2,2]+MCknn2[2,1])
MCknn2F = 2*MCknn2[2,2]/(2*MCknn2[2,2]+MCknn2[2,1]+2*MCknn2[1,2])
MCknn2specificite = MCknn2[2,2]/(MCknn2[2,2]+MCknn2[2,1])
knn2 = round(c(MCknn2err,MCknn2rappel,MCknn2precision,MCknn2F,MCknn2specificite),2)
predtest <- knn(train,test,cl,k=3)
MCknn3 = table(test$default,predtest)
MCknn3err = (MCknn3[2,1]+MCknn3[1,2])/sum(MCknn3)
MCknn3rappel = MCknn3[2,2]/(MCknn3[2,2]+MCknn3[1,2])
MCknn3precision = MCknn3[2,2]/(MCknn3[2,2]+MCknn3[2,1])
MCknn3F = 2*MCknn3[2,2]/(2*MCknn3[2,2]+MCknn3[2,1]+2*MCknn3[1,2])
MCknn3specificite = MCknn3[2,2]/(MCknn3[2,2]+MCknn3[2,1])
knn3 = round(c(MCknn3err,MCknn3rappel,MCknn3precision,MCknn3F,MCknn3specificite),2)
Logistic regression model
Preparing the data
data2$default <- as.factor(data2$default)
Defining the model
reglog <- glm(default~., family = binomial, data=train, control=list(maxit=1000, trace=TRUE, epsilon=1e-16))
preds <- predict(reglog, test, type='response')
optimal_cutoff <- ifelse(preds > 0.5, 1, 0)
summary(reglog)
##
## Call:
## glm(formula = default ~ ., family = binomial, data = train, control = list(maxit = 1000,
## trace = TRUE, epsilon = 1e-16))
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.3241 -0.6734 -0.3020 0.2628 2.6057
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.657904 0.664307 -2.496 0.0126 *
## age 0.044607 0.020375 2.189 0.0286 *
## employ -0.268156 0.037089 -7.230 4.82e-13 ***
## address -0.113424 0.027131 -4.181 2.91e-05 ***
## income -0.008652 0.008473 -1.021 0.3072
## debtinc 0.067861 0.035900 1.890 0.0587 .
## creddebt 0.611694 0.134228 4.557 5.19e-06 ***
## othdebt 0.080870 0.085357 0.947 0.3434
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 602.75 on 524 degrees of freedom
## Residual deviance: 418.16 on 517 degrees of freedom
## AIC: 434.16
##
## Number of Fisher Scoring iterations: 7
#confusion matrix
MCreg = table(test$default, optimal_cutoff)
MCregerr = (MCreg[2,1]+MCreg[1,2])/sum(MCreg)
MCregrappel = MCreg[2,2]/(MCreg[2,2]+MCreg[1,2])
MCregprecision = MCreg[2,2]/(MCreg[2,2]+MCreg[2,1])
MCregF = 2*MCreg[2,2]/(2*MCreg[2,2]+MCreg[2,1]+2*MCreg[1,2])
MCregspecificite = MCreg[2,2]/(MCreg[2,2]+MCreg[2,1])
reg = round(c(MCregerr,MCregrappel,MCregprecision,MCregF,MCregspecificite),2)
titles = c("Error rate","Recall","Accuracy","F-Score","Specificity")
data.frame(titles,lda,qda,knn1,knn2,knn3,PPM, reg)
## titles lda qda knn1 knn2 knn3 PPM reg
## 1 Error rate 0.19 0.21 0.29 0.30 0.24 0.54 0.18
## 2 Recall 0.70 0.66 0.46 0.42 0.56 0.22 0.68
## 3 Accuracy 0.50 0.46 0.46 0.35 0.39 0.14 0.59
## 4 F-Score 0.52 0.47 0.36 0.30 0.39 0.13 0.55
## 5 Specificity 0.50 0.46 0.46 0.35 0.39 0.14 0.59
Disciminant Analysis with cross-validation method Leave-One-Out
data2$default <- as.numeric(data2$default)-1
n = dim(data2)[1]
lda = 0
qda = 0
naive = 0
knn1 = 0
knn2 = 0
knn3 = 0
ppm = 0
for(i in 1:n) {
train <- data2[-i,]
test <- data2[i,]
# LDA #
model = predict(lda(default~.,train),test)
erlda = (data2$default[i] != model$class) + 0
MClda = table(model$class,test$default)
lda[i] = erlda
# QDA #
model2 = predict(qda(default~.,train),test)
erqda = (data2$default[i] != model2$class) + 0
qda[i] = erqda
# Naive Bayes #
model3 = predict(naiveBayes(default~.,train),test)
ernaive = (data2$default[i] != model3) + 0
naive[i] = ernaive
# KNN #
cl <- as.factor(train$default)
# Prediction K=1 #
predtest <- knn(train,test,cl, k=1)
# errors K=1 #
erknn1 = (data2$default[i] != predtest) + 0
knn1[i] = erknn1
# Prediction K=2 #
predtest <- knn(train,test,cl, k=2)
# errors K=2 #
erknn2 = (data2$default[i] != predtest) + 0
knn2[i] = erknn2
# Prediction K=3 #
predtest <- knn(train,test,cl, k=3)
# errors K=3 #
erknn3 = (data2$default[i] != predtest) + 0
knn3[i] = erknn3
# Prediction for closest mean #
no.age <- mean(train[train$default==0,]$age)
yes.age <- mean(train[train$default==1,]$age)
no.employ <- mean(train[train$default==0,]$employ)
yes.employ <- mean(train[train$default==1,]$employ)
no.address <- mean(train[train$default==0,]$address)
yes.address <- mean(train[train$default==1,]$address)
no.income <- mean(train[train$default==0,]$income)
yes.income <- mean(train[train$default==1,]$income)
no.debtinc <- mean(train[train$default==0,]$debtinc)
yes.debtinc <- mean(train[train$default==1,]$debtinc)
no.creddebt <- mean(train[train$default==0,]$creddebt)
yes.creddebt <- mean(train[train$default==1,]$creddebt)
no.othdebt <- mean(train[train$default==0,]$othdebt)
yes.othdebt <- mean(train[train$default==1,]$othdebt)
prediction <- function(x,z,a,b,c,d,e) {
if ((x-yes.age)^2+(z-yes.employ)^2+(a-yes.address)^2+
(b-yes.income)^2+(c-yes.debtinc)^2+(d-yes.creddebt)^2+
(e-yes.othdebt)^2 >
(x-no.age)^2+(z-no.employ)^2+(a-no.address)^2+
(b-no.income)^2+(c-no.debtinc)^2+(d-no.creddebt)^2+
(e-no.othdebt)^2)
{
return(1)
} else {return(0)}
}
pred <- prediction(test$age,test$employ,test$address, test$income, test$debtinc, test$creddebt, test$othdebt)
erppm = (data2$default[i] != pred) + 0
ppm[i] <- erppm
}
validationCroisée = c("taux d'erreur")
res = c(mean(lda),mean(qda),mean(naive),mean(knn1),mean(knn2),mean(knn3), mean(ppm))
lda = mean(lda)
qda = mean(qda)
naive = mean(naive)
knn1 = mean(knn1)
knn2 = mean(knn2)
knn3 = mean(knn3)
ppm = mean(ppm)
data.frame(validationCroisée,lda,qda,naive,knn1,knn2,knn3,ppm)
## validationCroisée lda qda naive knn1 knn2 knn3
## 1 taux d'erreur 0.1871429 0.2228571 0.2471429 0.2842857 0.2928571 0.2471429
## ppm
## 1 0.5414286
Here we can see that the model with the smallest error rate is the LDA model.
Using our best model for the prediction on the data
model = predict(lda(default~.,data2),apred)
model$class
## [1] 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
## [38] 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1
## [75] 0 0 0 0 0 0 0 1 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 0 0 1 0 0 1
## [112] 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0
## [149] 0 0
## Levels: 0 1
yes = 0
no = 0
for (i in 1:150){
if(model$class[i] == 1){
yes=yes+1
}else{
no=no+1
}
}
yes
## [1] 23
no
## [1] 127
prediction = yes/150;prediction
## [1] 0.1533333
So out of 150 people, 23 are likely to repay their credit and 127 are not likely to repay their credit, iow -> 15.3% of the population