The Goal of “Algorithmic and Complexity” 🧮
This class aims to train on finding a “good” algorithm for a given algorithmic problem. Which raises several questions:
- 🤔 Is there an algorithm to solve the problem? (computability, undecidability)
- 📚 Is the problem a “classic” one? (modeling, reformulation, knowledge)
- 💡 How to design an algorithm? (correct-by-construction algorithms, paradigms)
- ✅ Does the algorithm provide the right solution to the given problem? (algorithm correctness)
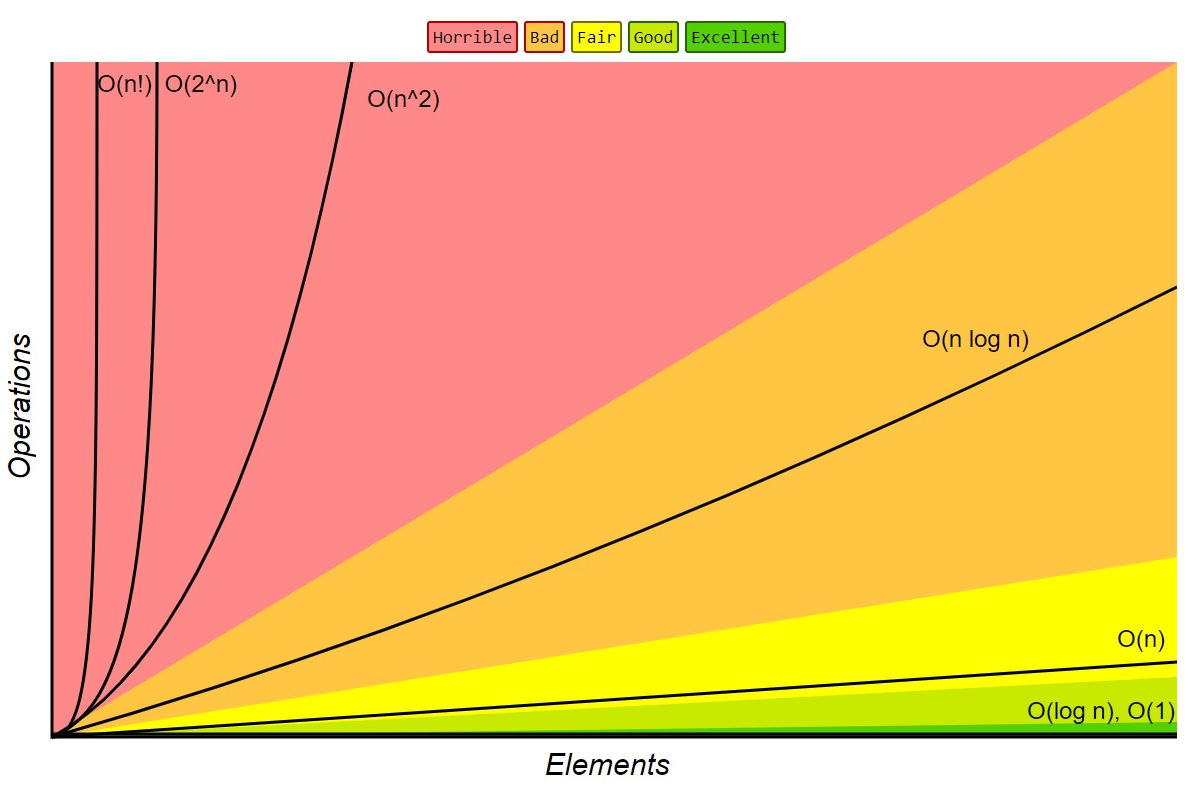
- ⏰ What about the resources used by the algorithm? (algorithm analysis)
- ⚙️ Is the algorithm reasonably efficient? Can we do better? What about the minimal resources needed to solve the problem? Can we hope for a “fast” algorithm? Is the problem - “hard”? (problem complexity)
- ❓ What to do when faced with a hard problem?
The course’s objective is to prepare you to answer these challenging questions, to train in “computational thinking,” and to develop the following skills:
- 🧐 Analyze a problem: modeling, reformulation, reduction, complexity
- 📝 Design an appropriate algorithmic solution, exact or approximate, using classic structures and paradigms effectively: dynamic programming, greedy algorithms, exhaustive - search, and heuristic methods.
- 📊 Analyze this solution: correctness, complexity.
The first document is the pdf report of the first assignement on basic algorithmic problems and computability with different notions of complexity (space and time).
The second deocument is the pdf report of the second assignement relating the use of different programming paradigms (Divise to Reign, Dynamix Programming, Greedy etc.)
The following document is the pdf report of the third assignement relating the use of polynomial reductions applied to the BinPacking problem.
And finally, the ultimate, the last, the absolute paroxism of this class : heuristics and meta-heuristics. Took us a while but here we are !